
Lesson: Sine curves and daylight
Class: “Mathematics Across the Sciences”
Professor: Meredith Greer, Associate Professor of Mathematics and Chair of the Program in Digital and Computational Studies
It’s an eternal question for generations of math students: How am I going to use this in the real world?
At Bates, Meredith Greer answers that question with an entire course, “Mathematics Across the Sciences.” It’s designed for both students who want to major in the natural sciences and need a strong math foundation, and those who need to fill a general education requirement.
The Lesson I Look Forward to Teaching
This is the first installment of “The Lesson I Look Forward to Teaching,” an occasional series on the lessons Bates professors know, from experience, are going to capture the attention of their students.
Students spend the course applying mathematics principles to real-life examples: They illustrate exponential growth by studying bacteria populations, measure earthquakes with logarithms, and use straight line equations to calculate the speed of human recall.
“It gives them a sense of all the ways math really is used,” says Greer, an associate professor of mathematics and chair of the Digital and Computational Studies program. “It’s not just a separate area of study alone, but it’s really relevant.”

Greer has taught “Mathematics Across the Sciences” in both fall and winter semesters, but it’s during the fall when she sees a special opportunity to make trigonometry click.
Toward the end of the semester, when temperatures are dropping and the sun sets depressingly close to 4 p.m., Greer explains trigonometric functions like sine and cosine.
Then, over the course of a class session or two, she has students collect data on the number of minutes of daylight Lewiston receives on days throughout the year. They do the same for Miami, then plot the data for both cities in an Excel chart.
The chart’s regularly occurring peaks (the highest amount of daylight a city gets in the summer) and valleys (the lowest in the winter) constitute a classic example of a sine curve, or oscillation.
Two results stand out. First, Lewiston’s curves from summer to winter and winter to summer are steeper than Miami’s. In other words, it’s true that when it gets darker in the fall, it gets darker faster.
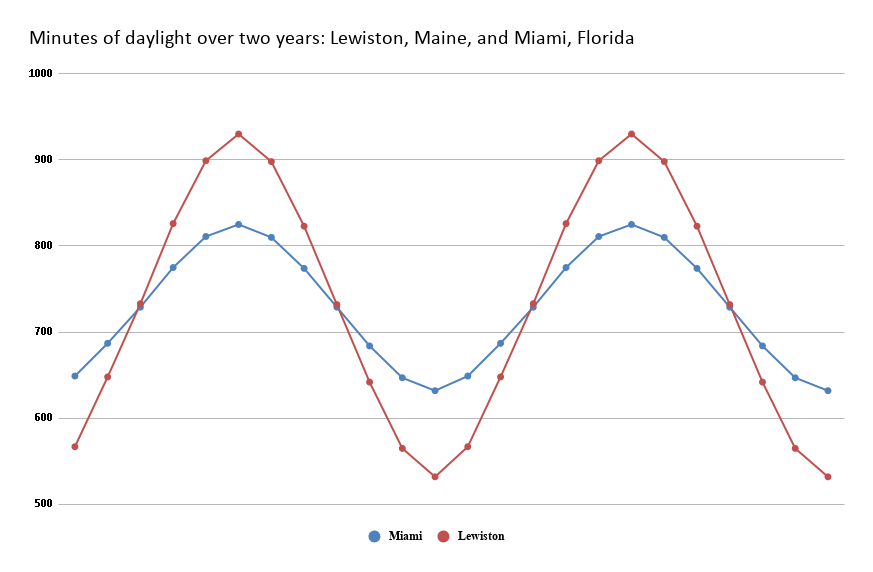
Now here’s the cool part. We all know that Lewiston hurts for daylight in the winter. The chart bears this out, showing lower valleys at the winter solstice for Lewiston (nearly nine hours of daylight) than for Miami (10.5 hours). In mathematical terms, the sine curve representing Lewiston has a greater amplitude.
The reverse is true in the summer: Lewiston’s peaks are higher than Miami’s; the northern city gets about 15.5 hours of daylight, compared to Miami’s nearly 14.
“What a lot of folks haven’t thought through is that if you get to the summer, they peak at this much lower level, and we peak much higher,” Greer says. “We have a lot more daylight in the summer.”
Why? It has to do with the tilt of the earth’s axis. The farther north or south you go, the more widely the amount of daylight varies. It’s why the poles have six-month alternating periods of daylight and dark.
For students, Greer says, working with daylight data at the end of the semester is one of the more immediate examples of the ways math can explain the world around us.
“A logarithmic function, a sine or cosine function, ex, 2x — they’re not just developed and done in math class and nowhere else,” she says. “They’re intrinsically related to nature. There’s a reason they were developed, and they mean something still.”




